
WILLIAM L. PALYA and MARK E. PEVEY
Jacksonville State University, Jacksonville, Alabama
Two experiments examined the effects of differences in the parameters of a clocked interfood interval on the obtained distribution of responding to the stimuli in that interval. In the first experiment, a 3 x 3 factorial design assessed the effects of the number of components and the durations of those components. Food was presented irrespective of behavior following 5,10, or 20 discrete stimuli across durations of 3, 6, or 12 sec each. Responding began at the approximate midpoint of the interval. More responding occurred in earlier portions of the last half of the interval as the number and the durations of individual stimuli decreased or as the overall interfood interval decreased. The second experiment, also a 3x3 factorial design, manipulated the probability and duration of food presentation following a 60-sec trial containing 10 discrete stimuli. A 2.0-, 3.5-, or 5.0-sec food presentation followed 100 %, 25 %, or 10 % of the trials. Responding again began at the approximate midpoint of the interval. More responding occurred in earlier portions of the last half of the interval only when both food duration and the proportion of reinforced trials increased. Both experiments therefore showed that the onset of responding occurs at the approximate midpoint of clocked interfood intervals in spite of a wide variety of CS and US manipulations.
A slide/tutorial version of this paper is available here.
Palya (1985) demonstrated that stimuli other than the one directly contiguous with food presentation would control chronic sign-tracking. The procedure partitioned a fixed 60-sec interfood interval into 10 6-sec periods, each signaled by a distinctive hue. This "interfood clock'' provided a measure of the sign-tracking controlled by each of the 10 stimuli that spanned the interfood interval. It reliably generated and maintained responding to fifth order stimuli. Response rates were successively higher to stimuli that were successively closer to food. The resulting behavior was attributable neither to hue nor to temporal generalization.
If responding on all but the final stimulus had eventually ceased, the finding would have been consistent with traditional notions of least effort, stimulus control, and discrimination (e.g., Ferster & Skinner, 1957, p. 266). Given that responding was chronically maintained to stimuli other than the final stimulus, however, it became important to develop a functional description of that behavior in terms of its schedule parameters. These data would allow a more adequate differentiation of the explanations for that responding.
Various interpretations for chronic responding to antecedent stimuli can be grouped roughly into those that explicitly include relative time as an essential feature and those that do not.
Typical absolute or nonrelativistic views might interpret Palya's data as demonstrating a delay-of-reinforcement gradient (Hull, 1952) or asymptotic associative strength for the absolute delay to food associated with each stimulus (Rescorla & Wagner, 1972). An absolute view could also invoke an additional process such as compound conditioning (Kehoe, 1982), conditioned reinforcement (Gollub, 1977), or higher order conditioning (Rashotte, 1981; Wickens, 1965) to account for the performance maintained by an interfood clock. This additional nonrelativistic factor would suggest that the stimulus associated with food presentation came to function as a reinforcer and conditioned behavior to the penultimate stimulus. The obtained data would be accounted for by extending this process to earlier and earlier stimuli and by invoking discrimination to account for the absence of responding to the very early stimuli in the interval.
Alternatively, a relativistic perspective stresses the importance of the relative temporal position in the interval associated with the onset of the stimulus of interest (Fantino & Navarick, 1974; Gibbon & Balsam, 1981; Jenkins, Barnes, & Barrera, 1981). This perspective would suggest that the responding controlled by a stimulus in an interfood clock was a function of the proportion of the interval remaining before food presentation rather than the absolute number of stimuli or seconds to food presentation. Unfortunately, neither view is complete. Both fail to predict with accuracy the extent to which the behavior is maintained by an interfood clock.
The documentation of how responding in an interfood clock varies as a function of traditional CS and US variables may shed light on the conditioning processes assumed to underlie behavior (e.g., Roberts, 1981). Variations in the number of clock stimuli per interval and the durations of these stimuli would indicate the importance of proportion of the interval, absolute time, and absolute number in the control of behavior. If responding in the interfood clock is distributed as if it were due to some absolute relationship, such as time to food or higher order conditioning, then it would be expected that a consistent number of stimuli or a consistent time from food would control responding across variations in the number and duration of individual clock stimuli. If, on the other hand, relative proportion were the primary determinant of responding, then the obtained responding should occupy a constant proportion of the various interfood intervals.
Variation in reinforcer parameters such as probability and duration of food presentation would indicate the importance of the strength of the reinforcer in maintaining early responding. If serial conditioning is maintained through a process such as higher order conditioning, then it should be affected by alterations in the reinforcer (Rashotte, Griffin, & Sisk, 1977). Alternatively, if the distribution of responding is maintained by the positioning of the reinforcer in time (Gibbon & Balsam, 1981), then those reinforcer variations should be relatively ineffective.
The present research was not designed to determine whether the obtained behavior was clearly Pavlovian or clearly operant, but rather was conducted in order to assess the effects of differences in the parameters of a clocked interfood interval on the obtained distribution of responding to the stimuli in that interval. A 3 X 3 factorial design determined the effects of the number of stimuli and the duration of those components. A second experiment, which was also a 3 X 3 factorial design, manipulated the probability and duration of food presentation following a 60-sec trial containing 10 discrete stimuli.
GENERAL METHOD
Subjects
Seventy-five adult domestic pigeons, obtained from a local supplier, were used as subjects. The 48 birds used in the initial part of Experiment 1 and again in Experiment 2 had had previous experience with various response contingencies and interval schedules containing stimuli correlated with the passage of time. The 27 birds used in the systematic replication of Experiment 1 were experimentally naive. All were housed under a 19:5 light:dark cycle in individual cages with free access to water. They were maintained at approximately 80% of their ad-lib weights with pelletized laying mash.
Apparatus
Five experimental chambers were used. The interior of each was 30 x 30 x 34 cm high and was painted white. A stimulus panel, with a feeder aperture 5 cm in diameter medially located 10 cm above the grid floor, served as one wall of the chamber. The food magazine was illuminated with a white light during food presentation. Three response keys, 2 cm in diameter, were located 9 cm apart, 25 cm above the grid. Only the center key was used. It required a force of approximately 15 g (0.15 N) to operate. The translucent Plexiglas key could be transilluminated by a stimulus projector containing color filters. The filters were the following Rosco theatrical gels: pink (829), red (26), orange (22), amber (615), yellow (12), green (874), yellow-green (878), turquoise (877), blue (657), purple (843), and magenta (49) . A Lee color-correcting filter (218) was used to produce white. Two houselights were located 10 cm apart, 32 cm above the grid floor. For small birds, the grid floor was raised 3 cm. Ventilation was provided by an exhaust fan mounted on the outside of the chamber. White-noise generators provided masking noise within each chamber as well as in the running room. Stimulus events were controlled and key pecks recorded by a computer system (Walter & Palya, 1984).
Procedure
Prior to an experimental procedure, the naive birds were exposed to a manually operated food magazine until they reliably approached from anywhere in the chamber and ate from the food hopper within 3 sec.
Both experiments involved variations of an interfood clock. A fixed interfood interval was segmented into time periods each of which was designated by a different key color. The basic procedure served as the common baseline for both experiments. The sequences of colors used were: for the 10-segment intervals, white, pink, red, orange, amber, yellow, green, turquoise, blue, purple; for the 5-segment intervals, pink, orange, yellow, turquoise, purple; and for the 20-segment intervals, white, white+pink, pink, pink+red, red, red+orange, orange, orange+amber, amber, orange+yellow, yellow, yellow-green, green, green+turquoise, turquoise, turquoise+blue, blue, blue+purple, purple, and magenta. Similar hues were adjacent in order to maximize their discriminability. Previous findings (Kaplan & Hearst, 1982; Palya, 1985) had indicated that stimulus generalization was not a primary determinant of responding to the antecedent stimuli in a serial compound.
In Experiment 1, a 2.5-sec food presentation occurred following the interval irrespective of behavior. In Experiment 2, the probability and duration of food presentation were manipulated. The houselights were off during food presentation and time-out. The clock sequence was repeated immediately following food offset or the scheduled time-out, without an intertrial interval. Throughout both experiments, sessions typically contained 40 to 50 food presentations, as determined by each bird's body weight that day. Some birds in Experiment 2 received fewer reinforcers, since session length was limited to 3 h.
EXPERIMENT 1
Method
Subjects and Apparatus. Seventy-five pigeons and five chambers were used. The 48 pigeons in the original procedure had had previous experimental experience. The 27 birds in the replication were naive.
Procedure. In the initial implementation of this experiment, a 3 x 3 factorial design varied the number of stimuli and the duration of those stimuli in an interfood clock. All birds were initially exposed to 12 sessions of the baseline procedure. Roughly similar groups were formed by assigning birds to groups on the basis of their response distributions during the preliminary exposure to an interfood clock. Each group of 6 pigeons was then exposed to intervals that contained 5, 10, or 20 stimuli that were each 3, 6, or 12 sec long.
Experiment 1 Procedures
| Group | Phase 1 (12 sessions) |
Phase 2 (15 sessions) |
Phase 3 (12 sessions) |
Replication (15 sessions) |
|---|---|---|---|---|
| 5-3 | 10-6(60) | 5-3(15) | 10-6(60) | 5-3(15) |
| 5-6 | 10-6(60) | 5-6(30) | 10-6(60) | 5-6(30) |
| 5-12 | 10-6(60) | 5-12(60) | 10-6(60) | 5-12(60) |
| 10-3 | 10-6(60) | 10-3(30) | 10-6(60) | 10-3(30) |
| 10-6 | 10-6(60) | |||
| 10-12 | 10-6(60) | 10-12(120) | 10-6(60) | 10-12(120) |
| 20-3 | 10-6(60) | 20-3(60) | 10-6(60) | 20-3(60) |
| 20-6 | 10-6(60) | 20-6(120) | 10-6(60) | 20-6(120) |
| 20-12 | 10-6(60) | 20-12(240) | 10-6(60) | 20-12(240) |
The procedural variations to which each group was exposed are listed in Table 1. The first number of each entry specifies the number of stimuli used; the second number specifies the duration of each stimulus. The resulting interfood interval is given in parentheses.
The common baseline procedure is indicated under the column labeled Phase I . In Phase 2, the number and/or durations of the stimuli in the interfood clock were altered for 15 sessions. For example, the 6 birds in Group 5-3 were shifted from a fixed 60 sec interfood clock containing 10 6-sec stimuli to a fixed I5-sec interfood clock containing 5 3-sec stimuli. In Phase 3, all groups were returned to the baseline procedure of the fixed 60 sec interfood clock, which contained 10 6-sec stimuli for an additional 12 sessions. A 10-6 group was not implemented in this initial procedure.
The parameter variations used in the initial 3 x 3 design were then replicated with naive birds. Nine groups of 3 birds each were exposed to intervals that contained 5, 10, or 20 stimuli, each 3, 6, or 12 sec long. The treatment conditions were implemented immediately following magazine training. The procedural variations to which each group in the replication was exposed are listed in the last column of Table 1.
Results and Discussion
Responding typically occurred to the stimuli presented during the last half of the clocked interfood interval. Responding began at the approximate midpoint of the interval with successively higher rates to successively later stimuli. The treatments demonstrated that a greater proportion of responding and a higher response rate occurred in the earlier fifths of the last half of the interval when the intervals contained fewer stimuli and stimuli of shorter duration, or simply when the overall interfood interval was shorter.
The impact of the parameter variations on responding to antecedent stimuli was assessed primarily using two measures. The index of onset denotes the onset of responding and is taken as the mean fifth in which the first 1% of responding was exceeded. This measure could be used as a behavioral index that defines the "positive," or "contiguous," portion of the trial, in that it denotes the portion of the interfood clock that supports responding. An index of 1.0 would indicate that responding started in the first fifth of the interval. An index of 3.0 would indicate that responding started in the middle fifth of the interval.
The index of curvature ( Fry, Kelleher, & Cook, 1960) characterizes the distribution of responding in an interval. It indicates the deviation from a constant rate. The cumulative record of a constant rate of responding would produce a right triangle with the base equal to the interfood interval duration. The index of curvature is a function of the difference between the area of the obtained cumulative record and a constant-rate record. This single summary of behavior in an interfood clock was used to index the degree to which antecedent stimuli controlled responding as the parameters of the clock were varied. An index of curvature of 0.80 would indicate that responding occurred only in the final fifth; an index of 0.00 would indicate that every stimulus maintained the same amount of behavior as did the final contiguous stimulus.
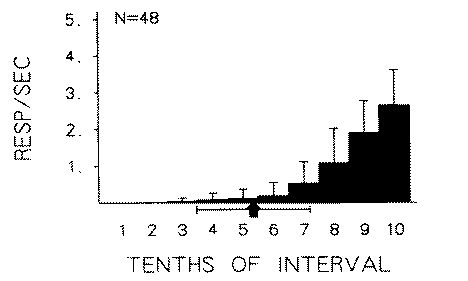
Measures of baseline behavior. Figure 1 presents the asymptotic rate at each of the 10 6-sec stimuli over the last five sessions of the initial baseline condition of the initial implementation of the 3 x 3 design for all birds combined. As can be seen, responding was reliably maintained by fifth-order stimuli, with successively higher rates to successively later stimuli in the second half of the interval. The mean point in the interval at which 1% of the responding was exceeded by the 48 birds under the baseline condition is depicted by an arrow under the x-axis. Tie bars designate 1 standard deviation across the 48 birds. The mean point of response onset, in terms of fifths of the interval, was 2.9 with a standard deviation of 0.93 fifths of an interval. The index of onset varied from 1.0 to 5.0 across individual birds and from 2.7 to 3.3 across groups. The index of curvature, based on fifths of the interval for this distribution of all birds combined, was 0.65 with a standard deviation of 0.10. The index of curvature varied from 0.41 to 0.80 across the 48 individual birds and from 0.60 to 0.68 across groups.
Measures of treatment effect. The impact of the parameter variations on the point in the interval at which responding began was assessed by a number of stimuli x duration of each stimulus analysis of variance. Neither the birds with previous experience nor the naive birds showed a reliable difference in the point of response onset.
To determine whether the treatments had an impact on the amount of responding maintained by the antecedent stimuli, the absolute rate of responding both in the birds with previous experience and in the naive birds was subjected to a number x duration x fifth of the interval analysis of variance. Data from the birds with previous experience showed a reliable difference in rate across fifths of the interval (p < .0001, [[omega]]2 = .62), indicating that response rates reliably increased across the interfood interval, as would be expected. The analysis also showed reliable interactions between fifth of interval and stimulus duration (p < .0001, [[omega]] = .03) and between fifth of interval and number of stimuli (p < .0006, [[omega]]2 = .02). These interactions indicated that both the number of stimuli in an interval and the durations of those stimuli altered the distribution of responding across the interfood interval. This meant that both the number of stimuli and their durations affected the amount of responding maintained by the antecedent stimuli in the second half of the interfood interval.
The distribution of responding obtained under the initial baseline was recovered following the treatment conditions. Taken together with the fact that the responding maintained by the stimuli following the midpoint showed both an increase and a decrease under the treatment conditions, the results indicated that the alteration in the distribution of responding was not simply due to extended experience with the interfood clock. Rather, the results indicated that the parameter variation affected the degree of responding maintained by the noncontiguous stimuli in the antecedent portion of the second half of the interfood clock.
A similar analysis of the distribution of responding across the interfood interval obtained from the naive birds showed essentially the same effects. There were a reliable difference in rate across fifths of the interval (p < .0001, [[omega]]2 = .32) and significant interactions of fifth times duration (p < .0001, [[omega]]2 = .09) and fifth times number of stimuli (p < .0l [[omega]]2 = .02). Additionally, there was a reliable duration main effect (p < .006, [[omega]]2 = .09). These results indicated that the number of stimuli and the durations of those stimuli in an interfood interval affected the degree to which the antecedent stimuli could acquire behavior in naive birds as well as maintain the behavior in birds with previous exposure to an interfood clock.
Figure 2 depicts the impact of the procedures on the amount of responding to the antecedent stimuli in the second half of the interfood interval. The index of curvature was used to summarize this effect. The earlier the responding in the interval, the lower the index. Since the point at which responding started as well as the response rates in the final stimulus of the interval were not reliably different, the index of curvature indicated the degree to which schedule parameters supported responding to the antecedent stimuli of the last half of the interfood clock. The left frame shows the results obtained with the experienced birds, and the right frame shows the data for the replication with the naive birds. Stimulus duration is depicted across the x-axes and number of stimuli in each interval is represented back the z-axes. The height of the bar at each intersection in each frame designates the dependent measure for the group exposed to that combination of conditions. As can be seen, the same general relationship was evident in both the experienced and the naive birds.
The left frame presents the index of curvature based on rates during the treatment condition for the experienced birds. A plane fitted by multiple regression to these data of the eight procedural variations accounted for 87% (p < .001, [[omega]]2= .80) of the total variance [23% (p < .00l, [[omega]]2 = .20) when including bird-to-bird variability]. An analysis of variance indicated that only the main effect for duration of stimuli was statistically reliable (p < .005, [[omega]]2 = .16). The unfilled bar in this frame is included as a point of reference. It depicts the mean index of curvature for the 48 experienced birds during their initial baseline condition.
The right frame depicts the data obtained from naive birds exposed to the same treatment conditions. This frame presents indices of curvature based on the rates obtained during the treatment conditions, the only conditions implemented with these birds. The multiple regression plane accounted for 64% (p > .04, [[omega]]2= .49) of the total variance (34% (p < .003, [[omega]]2= .32) when including bird-to-bird variability]. An analysis of variance indicated that only the main effect for number of stimuli was statistically reliable (p < .004, [[omega]]2 = .29). This frame shows that generally the same effect occurred with naive birds as had occurred with birds with previous experience. The notable exception was the low indices of curvature in the group receiving 10 stimuli at 12 sec each. Examination of the individual data for the birds in this group indicated that this effect was attributable to the very low response rates established by that procedure. These birds responded only rarely and at a relatively equal rate throughout the last half of the interval. This behavior necessarily produced an inordinately low index of curvature and is evident in the individual data presented in Figure 5.
The obtained results can also be viewed in terms of index of curvature as a function of the single variable "overall interfood interval" rather than as a joint function of stimulus number and stimulus duration. Figure 3 depicts the amount of responding maintained by the antecedent stimuli in that form. The top frame shows the results obtained with the experienced birds, and the bottom frame shows the data for the replication with naive birds. The data for the eight treatment conditions are arranged on the x-axis with respect to overall interfood interval; the shorter intervals are to the left, and the longer intervals are to the right. Two different treatment groups provide data for the 30-, 60-, and 120-sec interfood intervals. An open bar representing the mean index of curvature during baseline conditions across all 48 birds combined is also included in the top frame for comparison. The heights of the bars designate the dependent measure for the group exposed to the combination of conditions that produced the indicated interfood interval.
Both frames show that as the overall interfood interval increased, the index of curvature increased. This indicates that fewer responses occurred in the earlier portions of the second half of the longer intervals. Overall interfood interval accounted for 58% (p < .004, [[omega]]2 = .61) and 58% (p < .002, [[omega]]2 = .65) of the total variance in the indices of curvature for the data in the top and bottom frames, respectively [14% (p < .006, [[omega]]2 = .12) and 36% (p < .001, [[omega]]2 = .33) when including bird-to-bird variability]. An analysis of variance on these data indicated a reliable increase in index of curvature as the overall interval increased (p < .002, [[omega]]2 = .25, and p < .0l, [[omega]]2 = .32, respectively).
Figure 5. Response rate as a function of proportion of interval, stimuli preceding food presentation, and seconds preceding food presentation. These data are for the birds without previous experimental histories. They are presented in the same format and group order as were used in Figure 4.
The distribution of response rates across the interfood interval for each bird under each treatment condition is presented in Figures 4 and 5. Figure 4 presents the data for the birds with previous experience; Figure 5 presents the data for the naive birds. The left frames in both figures present the response distributions in terms of proportion of the interfood interval. The center frames in both figures present the same distributions in terms of number of stimuli preceding food presentation. The right frames present the data in terms of seconds preceding food presentation. These figures provide an indication of the roles that proportion of interval, absolute number of stimuli until food, and absolute time until food presentation have on the amount of responding maintained by each stimulus in the interval. Additionally, they demonstrate that the group statistics adequately represent the data for individual birds.
The data for each of the 48 birds are depicted back the z-axes. The height of each function in each frame designates the response rate for that bird at that point in the interval. Both the birds within each treatment condition and the conditions themselves have been ordered in terms of the amount of responding in the interval. As can be seen, the results in the left, or "proportion,'' frames are in terms of decreasing overall interfood interval. The results in the center, or "stimuli preceding food," frames are in terms of increasing number of stimuli of decreasing duration. The results in the right, or "seconds preceding food,'' frames are in terms of increasing overall interfood interval.
The data in terms of proportion of the interval for the experienced birds are presented in the left frame of Figure 4. It shows that even though approximately 1% of the responding may have occurred by the end of the middle fifth, a higher response rate was clearly evident in earlier fifths of the interval when the intervals contained fewer stimuli and when those stimuli were shorter. This can be seen by comparing the upper and lower portions of the left frame. This proportion effect occurred in spite of the fact that intervals with more stimuli of shorter durations maintained responding to more individual stimuli (upper portion of center frame), and longer interfood intervals maintained responding for longer absolute times (upper portion of the right frame).
To facilitate comparison, the data for the naive birds, which are presented in Figure 5, were arranged in the same group order as the data for the experienced birds presented in Figure 4. The data for these birds show a somewhat different picture. Both the very short intervals and the very long intervals failed to control substantial keypecking. The major inconsistency with the original implementation of these procedures with experienced birds (Figure 4) was the relatively weak responding in the very short intervals (upper portion of left frame). This difference is not entirely surprising, however, in that it is consistent with other findings that show weak effects when acquisition measures are used with very short interfood intervals (Jenkins et al., 1981; Terrace, Gibbon, Farrell, & Baldock, 1975). It may be that these parameters did not establish keypecking as the predominant terminal behavior (Staddon & Simmelhag, 1971). The two remaining frames in Figure 5 show that, like the birds with previous experience, the naive birds generally responded to more stimuli in intervals that contained more stimuli of shorter duration, and responded for longer absolute durations when the overall interfood intervals were longer.
In sum, the results indicate that responding in a clocked interfood interval begins at the approximate midpoint of the interval regardless of the number of clock stimuli and regardless of their duration. Moreover, a large portion of the variability in response distributions could be accounted for by nothing more than the interfood interval duration. This finding is generally consistent with views that suggest that interval effects are relative (Dews, 1970; Fantino, 1977; Gibbon & Balsam, 1981; Jenkins, 1984). However, the obtained results were not entirely consistent with those relativistic perspectives. Figures 4 and 5 demonstrate that the response distributions were affected to a degree by both the number of stimuli in an interval and their duration. Those figures showed that as the number or duration of stimuli decreased, more responding occurred in earlier portions of the interval.
EXPERIMENT 2
Experiment 1 had assessed the effects of stimulus number and duration on the amount of responding maintained by the stimuli in an interfood clock. This second experiment varied the probability and duration of food presentation. Such reinforcer manipulations would be expected to alter the ability of interfood clock stimuli to control behavior if a process like higher order conditioning were the major determinant of that behavior. If, on the other hand, responding were primarily determined by the interfood interval duration, then those manipulations would be relatively ineffective.
Method
Subjects and Apparatus. Forty-five of the 48 birds used in the initial part of Experiment I and five chambers were used in this experiment.
Procedure. A 3 x3 factorial design varied the probability and duration of food presentation following a 60-sec interfood interval segmented into 10 discriminable time periods. All birds were initially exposed to 10 sessions of the baseline procedure. Roughly similar groups were formed by assigning birds to groups on the basis of their response distributions during Phase 3 of the preceding experiment. Each group of 5 birds was then exposed to intervals (10 6-sec stimuli) followed by 2.0, 3.5, or 5.0 sec of food following 100%, 25%, or 10% of the trials.
Phase 2 altered the probability and/or duration of the food presentation following the interfood clock for 18 sessions. For example, the 5 birds in one of the nine groups were shifted from a fixed 60-sec interfood clock containing 10 6-sec stimuli followed by a 2.5-sec food presentation to an interval containing 10 6-sec stimuli followed by a 5-sec food presentation on 10% of the trials. All groups were subsequently returned to the baseline procedure of an interfood clock followed by a 2.5-sec food presentation on every trial for an additional 12 sessions.
Results and Discussion
In general, the distribution of responding across the interfood interval was the same as that found in the previous experiment. Responding typically began at the approximate midpoint of the interval, with successively later stimuli controlling successively higher rates. The data indicated that more responding occurred to earlier stimuli in the last half of the interval only when both the food duration and the proportion of reinforced trials increased.
Measures of baseline behavior. The data obtained under the baseline condition were essentially identical to the baseline data in the preceding experiment. The mean point of response onset in terms of fifths of the interval was 2.9, with a standard deviation of 1.1 fifths of an interval. This varied from 1.0 to 5.0 across individual birds and from 2.6 to 3.4 across groups. The index of curvature based on fifths of the interval for all birds combined was 0.66, with a standard deviation of 0.10. The index of curvature varied from 0.34 to 0.80 across the 45 individual birds and from 0.60 to 0.73 across groups.
Measures of treatment effect. The effect of this procedure on the point of response onset was assessed with a probability of food presentation times duration of food presentation analysis of variance. It indicated that there were no reliable probability or duration effects on the point of response onset.
The absolute rate of responding in each fifth of the interval was assessed with a probability times duration times fifth of the interval analysis of variance. As would be expected, the analysis indicated a reliable fifth of the interval effect (p < .000l, [[omega]]2 = .67). The analysis gave little evidence that either probability or duration of food presentation in isolation had a reliable effect on the distribution of responding in the interfood interval. However, there were significant probability times duration ( p < .01, [[omega]]2 = .0l ) and probability times duration times fifth (p < .02, [[omega]]2 = .02) interactions. These interactions indicate that when combined, probability and duration are sufficient to alter the distribution of responding. Details of this effect are presented and discussed in subsequent paragraphs.
Figure 6 depicts the impact of the procedures on the index of curvature for each of the nine groups. The duration of the food presentation is presented across the x-axis and the probability of food is depicted back the z-axis. The index of curvature in the treatment phase for each group is indicated by the height of the bar at that intersection.
Although a plane fitted by multiple regression to the mean data accounted for 49% of the total variance, it was not reliable. The plane based on the data of individual birds accounted for 15% (p < .04, [[omega]]2 = .10) of the variability. The reliability of these results was assessed with a probability times duration analysis of variance. The analysis indicated neither probability nor duration of food presentation had a reliable effect.
Figure 7 presents the index of curvature as a function of the single dimension "mean seconds of food per 60-sec clock cycle." This measure is analogous to that of reinforcement time, offered by Premack (1965) and Ten Eyck (1970). The mean amount of food per clock cycle increases to the right along the x-axis. The data from the group with the smallest mean seconds of food per clock (probability = .10, duration = 2.0 sec) are presented on the left. The data from the group with the most food per clock (probability = 1.0, duration = 5.0 sec) are presented on the right. The heights of the bars depict the index of curvature during the treatment condition for each group. As can be seen, there was a systematic increase in the amount of responding to the stimuli in the early portion of the second half of the interval as the mean seconds of food following a clock cycle increased (i.e., the index of curvature decreased). Mean seconds of food per clock accounted for 78% (p < .002, [[omega]]2 = .73) of the total variance in the data. The same analysis when including bird-to-bird variability was 16% (p < .007, [[omega]]2 = .14). An analysis of variance on these data indicated a reliable decrease in index of curvature as the mean seconds of food per clock increased (p < .03, [[omega]]2 = .22). This finding is consistent with the reliable probability times duration times fifth of interval interaction obtained in the analysis of the response rate across fifths of the interfood interval.
The distribution of response rates across the interfood clock for each bird under each treatment condition is presented in Figure 8. The figure demonstrates that the group statistics adequately represent the data for the individual birds. Since all birds were exposed to the same interfood clock, the x-axis can be seen as depicting proportion of the interval, consecutive stimuli, or the duration. The data for each of the 45 birds are depicted back the z-axis. The height of each function designates the response rate for that bird at that point in the interval.
Both the birds within each treatment condition and the conditions themselves are ordered roughly in terms of the amounts of responding in the interval. This results in an ordering of the data in terms of mean seconds of food presentation per clock. The birds receiving only 2.0 sec of food on 10% of the clock cycles are presented first. The upper portion of the frame shows the data for the group receiving 5 sec of food following every clock cycle. No consistent trends appear when the data are viewed independently with respect to probability or duration of food presentation. In contrast, when the data are arranged in terms of mean seconds of food per clock, as was the case in Figure 7, the figure shows an orderly increase in the responding maintained by the stimuli in earlier portions of the interval. The magnitude of the effect, however, is much less than that obtained when number or duration of the component stimuli was varied.
In sum, when both probability and duration of food presentation were increased ( Baum & Rachlin, 1969; Premack, 1969), there was a reliable increase in the amount of responding supported by the antecedent stimuli in the last half of the interfood interval. However, variations in either probability or duration of food presentation alone had little effect on the distribution of responding. The relative ineffectiveness of variations in reinforcement (Rashotte, 1981), especially when food duration was manipulated, is consistent with the findings of other studies that have varied reinforcement ( Balsam, Brownstein, & Shull, 1978; Balsam & Payne, 1979; O'Connell & Rashotte 1979).
These data support the views (e.g., Gibbon & Balsam, 1981) that suggest that behavior in an interval is importantly determined by the relative time in that interval and is, in general, unaffected by alterations in the duration or probability of food presentation. Gibbon and Balsam had argued that responding would occur to a stimulus contiguous with the reinforcer when that stimulus occupied less than half the interfood interval. Variations in reinforcer parameters, such as its intensity, quality, or duration, were thought to be irrelevant because those manipulations did not affect the ratio of the interfood interval to the trial stimulus. Similarly, because it left the ratio of trial duration to interfood interval unchanged, partial reinforcement was not expected to affect the distribution of responding either. Probabilistic reinforcement simply multiplies both the trial stimulus duration and the interfood interval by the same constant.
In contrast, the Rescorla-Wagner model (Rescorla & Wagner, 1972) holds that manipulation of reinforcer parameters would have an effect on the degree of responding maintained by the reinforcer. Those alterations would be expected to affect the asymptotic level of responding that could be maintained by the reinforcer and, as a result, would alter the responding maintained by an antecedent stimulus in a higher order conditioning preparation (Rescorla, 1979, 1980).
Although a simple temporal relativity position did not account for all of the variability in the present data, a reasonable description of the amount of responding maintained by the antecedent stimuli in both experiments could be made on the basis of nothing more than the interfood interval duration. Index of curvature as a function of interfood interval duration yielded an r2 of .59 for group data (p < .000l, [[omega]]2 = .56) and an r2 of .27 for individual data (p < .0001, [[omega]]2 = .26) across the 26 conditions of both experiments.
GENERAL DISCUSSION
The major finding of the present study was that responding to an interfood clock typically begins at the approximate midpoint of the interval in spite of large variations in CS and US parameters. Additionally, response rates to the final stimulus are relatively similar across the same range. The amount of responding controlled by stimuli in the early portions of the second half of an interval is affected by variations in the number of stimuli making up the clock, their duration, and the duration and probability of food delivery following the last stimulus. More responding occurred in early portions of the second half of the interval when there were fewer stimuli, of shorter duration, that were followed by more food more often. However, each of these manipulations also indirectly varied the overall interfood interval. It was shown that the interfood-interval duration alone could account for 59% of the group-to-group variability and 27% of the bird-to-bird variability across the 26 conditions of both experiments.
Palya (1985) demonstrated that it was unlikely that the behavior maintained by antecedent stimuli in an interfood clock was the result of primarily nonassociative factors, such as hue or temporal generalization. He showed that the increasing rate to the antecedent stimuli in the latter half of the interval could be maintained by a variety of sequences if the component stimuli were consistently ordered, but not if the stimuli within each interval were randomly ordered. If the responding maintained by the stimuli in the earlier portions of the interval were due to the similarity of those clock stimuli to the stimulus contiguous with food presentation, then that factor would have been apparent when the stimuli were presented in other sequences. If the interfood interval had effectively only a single stimulus, then the increase in responding across the last half of the interval could seemingly be explained by reference to temporal confusion or inability to discriminate temporal stimuli. Such an explanation is tautological, and was explicitly rejected when randomized clock stimuli failed to maintain responding.
The results were therefore more appropriately seen as indicating primarily an associative effect. Whether that associative effect is best characterized as Pavlovian or operant has been argued in detail elsewhere (Hearst & Jenkins, 1974; Locurto, 1981; Terrace, 1981), and was not addressed. Furthermore, the present paper was not intended to determine the nature of the molecular mechanism that supported responding to the antecedent stimuli (e.g., Kehoe, 1982). Rather, the present research was intended to determine how behavior to the antecedent stimuli in an interfood clock varied as a function of parameters of the clock and whether that variation was best characterized as a function of absolute values, such as seconds or stimuli to food presentation, or as some relative effect, such as portion of the interval.
The chronic responding to the antecedent stimuli in an interfood clock could be maintained by the absolute delay to food or by the number of stimuli to food. One such interpretation (Hull, 1952) would suggest that all of the events throughout the interfood clock are eventually followed by food presentation. The only difference between them is that food follows the events in the initial portions of the interval after a longer delay. The distribution of responding in an interfood clock would follow from this perspective without additional processes, in that absolute proximity to food presentation would be the only relevant determinant of responding. However, the findings of the present study, with a variety of interfood clocks, are consistent with the literature (e.g., Dews, 1970) in showing that behavior in an interfood interval is primarily a function of relative time rather than absolute delay to food presentation.
If it is presumed that responding will occur only to the stimulus in the presence of which food is presented (Ferster & Skinner, 1957; Spence, 1956), additional processes must be invoked to account for the chronic responding to stimuli in the early portion of the second half of the interval. Higher order conditioning or conditioned reinforcement would be potential explanations. These views suggest that a stimulus associated with food presentation would become a reinforcer itself, and would thereby condition responding to the penultimate stimulus. Unfortunately, this process could be said to occur to whatever extent was necessary to account for the data, and is therefore insufficient, as such, to provide much help in predicting the early responding in an interfood clock. Without additional specification, the explanation is empty ( Byrd, 1971).
Data obtained in Experiment 2 of the present study further emphasizes the insufficiency of simply invoking a process such as higher order conditioning whenever responding occurs to stimuli other than the stimulus directly contiguous with the reinforcer. Even though it is based on theoretical considerations rather than on extensive data, it would typically be expected that variation in the probability and duration of food would alter the ability of the final stimulus to function as a reinforcer ( Lendenmann, Myers, & Fantino, 1982; Rescorla, 1979). Variations in the reinforcing effectiveness of the final stimulus would, in turn, be expected to affect the response rates to earlier stimuli. However, within the range of values used, the present data show that neither probability nor duration of food presentation alone altered the amount of responding maintained by the antecedent stimuli.
The present study could be seen as empirically quantifying the expected extent of higher order conditioning or conditioned reinforcement with changes in CS and US parameters. The data demonstrate that those effects, like autoshaping (Gibbon & Balsam, 1981) and fixed-interval responding (Dews, 1970), are best seen as a relative process importantly controlled by the interfood interval rather than simply by the number of links preceding reinforcement. In fact, the present data indicate that some degree of responding can be expected to extend to the approximate midpoint of the interval, independently of the absolute number of stimuli or the absolute delay to food presentation and independently of the strength of the primary reinforcer.
There is, however, a trap in suggesting that the obtained distribution of responding provides an empirical specification of the relative contiguity of various portions of the interval to food presentation or of the relative extent of higher order conditioning and conditioned reinforcement. By defining the processes in terms of obtained responding, the ability to then nontautologically explain responding by invoking those processes is lost. The present data permit only the observation that if delay of reinforcement, higher order conditioning, or conditioned reinforcement is subsequently shown to be responsible for the responding to antecedent stimuli, then the present data describe its functional effectiveness.
Chronic responding to the stimuli in the early portions of the second half of the interval could also be accounted for by postulating an additional source of reinforcement in the interval. Egger and Miller (1962, 1963) suggested that the information provided by the first reliable predictor of food in a stimulus sequence preceding food presentation resulted in a greater reinforcing effectiveness for that stimulus. Responding to the elements of an interfood clock could be seen as a function of information in two ways. An early clock stimulus could function as a reinforcer, as originally suggested by Egger and Miller, and reinforce operants in the preceding stimulus, or that information could be an elicitor of stimulus-directed pecking (Allaway, 1971).
Neither of these information positions would have predicted a peak of responding at the end of the interfood clock. Egger and Miller's (1962, 1963) view, as well as information views in general, attempt to account for the finding that earlier stimuli often come to function as more effective reinforcers than contiguous stimuli. The obtained results were exactly opposite to those for which information views were advanced. If it is suggested that there is limited information in the system, and the initial stimulus provides most of the available information, then each subsequent stimulus must provide somewhat less. By the latter portions of the interval there should be little uncertainty remaining, and therefore little reinforcing or eliciting capacity (Cantor, 1981).
A second major flaw with the use of information as an explanation for responding in the interfood interval is that information views provide no a priori rationale for specifying which stimuli in an interfood clock provide information about impending food presentation and which stimuli provide information concerning the continuing absence of food. Presumably, stimuli informing about food would control responding, whereas those informing about no food would not.
The present data could be viewed as resolving this second inadequacy by documenting which stimuli control responding and to what extent. For example, the present results could be taken to indicate that stimuli in the last half of an interval provide positive information. However, it would still be necessary to resolve the discrepancy between the increasing response rates to successive clock stimuli and typical information positions before assuming that the distribution of responding resulted from the additional effects of information as a reinforcer or elicitor.
Gibbon and Balsam (1981) offered a temporal relativity account of autoshaping which provided a framework within which the present findings could be understood. They specified the results to be expected with stimuli associated with various portions of the interfood interval. Strictly speaking, their analysis applies only to procedures that partition the trial into dichotomous components, one portion during which no food is presented and the other contiguous with food presentation. They did not deal with multistimulus trials, and therefore made no explicit predictions applicable to an interfood clock. In spite of this, however, their perspective remains relevant to the current analysis. The present data indicate that their position can be generalized to a multistimulus case even though there are a few differences.
Gibbon and Balsam (1981) contended that the duration of the trial with respect to the overall interfood interval determines expectancy, which in turn determines responding. To simplify the task of making predictions, expectancy was assumed to be equal across the duration of the contiguous trial stimulus. As Gibbon and Balsam suggested, a single index describing an entire positive trial may be insufficient following extensive experience with the schedule. Gibbon, Farrell, Locurto, Duncan, and Terrace (1980) obtained an increasing response rate across a single stimulus trial, suggesting an increasing expectancy. The present study, as well as that of Palya (1985), corroborated this finding by demonstrating scalloped responding, and therefore presumably increasing expectancy, across the last half or positive portion of the interfood interval even when the various portions of the interval were made explicitly different.
Gibbon and Balsam suggested that it might be that only the final contiguous stimulus would control responding (Gibbon & Balsam, 1981). This view is comparable to the position of Ferster and Skinner (1957), who stated that responding would be expected to occur only to the extent that the stimulus context was similar to that at food presentation. This implication was borne out neither by the present data nor by a variety of other studies ( Newlin & LoLordo, 1976; Palya, 1985; Ricci, 1973). The present results indicate that virtually all clock stimuli associated with the last half of an interval control responding to some extent, whereas those occurring before the midpoint typically do not.
The present study showed that the response rate to the final stimulus in the sequence (i.e., the stimulus contiguous with food presentation) was not altered by variations in either CS or US parameters. However, the data also showed that the amount of responding to the antecedent stimuli was affected by some of those manipulations. These findings indicated that the response rate to the final stimulus in an interfood clock was not controlled by its duration relative to the interfood interval, and that the response rate at the final stimulus, in turn, did not determine the rate controlled by the stimuli preceding it.
These findings and Gibbon and Balsam's (1981) position can be brought into coherence simply by considering the last half of the interfood interval as the positive trial. Gibbon and Balsam's determination of the middle of the interval as the point at which a single contiguous trial stimulus begins to support responding is therefore a special case of the present findings, which showed that some degree of responding occurs to any stimulus associated with only the second half of an interfood interval. This perspective would be analogous to Dews's (1962) and Jenkins's (1970) views of reinforcement in interval schedules.
Gibbon et al. (1980) demonstrated that acquisition of responding to a single trial stimulus was a function of the portion of an interval occupied by the contiguous trial stimulus. The number of trials to the criterion was a function of the relative position of the trial onset in the interfood interval. The present interfood clock procedure provided a within-subject/within-trial assessment of the degree to which various temporal portions of an interfood interval maintain responding. The obtained function based on response rates at discriminably different clock stimuli within an interfood interval is generally consistent with between-group comparisons that depict trials to acquisition as a function of proportion of interval occupied by a single trial stimulus contiguous with food presentation (Gibbon & Balsam, 1981).
The present research, like Dews's (1970), Gibbon and Balsam's (1981), and Jenkins's (1970), found that a wide variety of potentially important parameters were not of great importance in controlling the onset of responding in an interfood interval. The temporal placement of food presentation has the dominant influence on the pattern of responding across time (Zeiler, 1977). The present data show that even when the interval is partitioned into discriminable segments, the interfood interval controls increasing amounts of behavior in consecutive portions of the second half of the interfood interval. Since nonassociative spread of effect cannot account for the obtained distribution of responding, the obtained distribution of responding may reflect the associative limit for those portions of the interfood interval.
ALLAWAY, T. A. (1971). Attention, information, and autoshaping. Unpublished doctoral dissertation, University of Pennsylvania, Philadelphia.
BALSAM, P. D., Brownstein, A. J., & SHULL, R. L. (1978). The effects of duration of grain presentation on automaintenance. Journal of the Experimental Analysis of Behavior, 29, 27-36.
BALSAM, P. D., & PAYNE, D. (1979). Intertrial interval and unconditioned stimulus durations in autoshaping. Animal Learning & Behavior, 7, 477482.
BAUM W. M., & RACHLIN, H. C. (1969). Choice as time allocation. Journal of the Experimental Analysis of Behavior, 12, 861-874.
BYRD, L. D. (l97l). Responding in the pigeon under chained schedules of food presentation: The repetition of a stimulus during alternate components. Journal of the Experimental Analysis of Behavior, 16, 31-38.
CANTOR, M. B. (1981). Information theory: A solution to two big problems in the analysis of behaviour. In P. H. Harzem & M. D. Zeiler (Eds.), Predictability, correlation, and contiguity (pp. 286-320). New York: Wiley.
DEWS, P. B. (1962). The effects of multiple S[[Delta]] periods on responding on a fixed-interval schedule. Journal of the Experimental Analysis of Behavior, 5, 369-374.
DEWS, P. B. (1970). The theory of fixed-interval responding. In W. N. Schoenfeld (Ed.), The theory of reinforcement schedules (pp. 43-61). New York: Appleton-Century-Crofts.
EGGER, D. M., & MILLER, N. E. (1962). Secondary reinforcement in rats as a function of information value and reliability of the stimulus. Journal of Experimental Psychology, 64, 97-104.
EGGER, D. M., & MILLER, N. E. (1963). When is a reward reinforcing? An experimental study of the information hypothesis. Journal of Comparative and Physiological Psychology, 56, 132-137.
FANTINO, E. (1977). Conditioned reinforcement: Choice and information. In W. K. Honig & J. E. R. Staddon (Eds.), Handbook of operant behavior (pp. 313-339). Englewood Cliffs, NJ: Prentice-Hall.
FANTINO, E., & NAVARICK, D. (1974). Recent developments in choice. In G. H Bower (Ed.), The psychology of learning and motivation (Vol. 8, pp. 147-185). New York: Academic Press.
FERSTER, C . B ., & SKINNER, B . F . ( 1957) . Schedules of reinforcement . New York: Appleton-Century-Crofts.
FRY, W., KELLEHER, R. T., & COOK, L. (1960). A mathematical index of performance on fixed-interval schedules of reinforcement. Journal of the Experimental Analysis of Behavior, 3, 193-199.
GIBBON, J., & BALSAM, P. (1981). Spreading association in time. In C. M. Locurto, H. S Terrace, & J. Gibbon (Eds.), Autoshaping and conditioning theory (pp. 219-253). New York: Academic Press.
GIBBON, J., FARRELL, L., LOCURTO, C. M., DUNCAN, H. J., & TERRACE, H. S. (1980). Partial reinforcement in autoshapmg with pigeons. Animal Learning & Behavior, 8, 45-59.
GOLLUB, L. R. (1977). Conditioned reinforcement: Schedule effects. In W. K Honig & J. E. R. Staddon (Eds.), Handbook of operant behavior. Englewood Cliffs, NJ: Prentice-Hall.
HEARST, E., & JENKINS, H. M. (1974). Sign-tracking: The stimulus-reinforcer relation and directed action. Austin, TX: Psychonomic Society.
HULL, C. L. (1952). A behavior system. New Haven: Yale University Press.
JENKINS, H. M. (1970). Sequential organization in schedules of reinforcement. In W. N. Schoenfeld (Ed.), The theory of reinforcement schedules (pp. 63-109). New York: Appleton-Century-Crofts.
JENKINS, H. M. (1984). Time and contingency in classical conditioning. In J. Gibbon & L. Allan (Eds.), Annals of the New York Academy of Sciences: Vol. 423. Timing and time perception (pp. 242-253). New York: New York Academy of Sciences.
JENKINS, H. M., BARNES, R. A., & BARRERA, F. J. (1981). Why autoshaping depends on trial spacing. In C. M. Locurto, H. S. Terrace, & J. Gibbon (Eds.), Autoshaping and conditioning theory (pp. 255284). New York: Academic Press.
KAPLAN, P. S., & HEARST, E. (1982). Bridging temporal gaps between CS and US in autoshaping: Insertion of other stimuli before, during, and after CS. Journal of Experimental Psychology: Animal Behavior Processes, 8, 187-203.
KEHOE, E. J. (1982). Conditioning with serial compound stimuli: Theoretical and empirical issues. Experimental Animal Behaviour, 1, 30-65.
LENDENMANN, K. W., MYERS, D. L., & FANTINO, E. (1982). Effects of reinforcer duration on responding in two-link chained interval schedules. Journal of the Experimental Analysis of Behavior, 37, 217-222.
LOCURTO, C . M . ( 1981 ) . Contributions of autoshaping to the partitioning of conditioned behavior. In C. M. Locurto, H. S. Terrace, & J. Gibbon (Eds.), Autoshaping and conditioning theory (pp. 1-18). New York: Academic Press.
NEWLIN, R J., & LOLORDO, V. M (1976). A comparison of pecking generated by serial, delay, and trace autoshaping procedures. Journal of the Experimental Analysis of Behavior, 25, 227-241.
O'CONNELL, J. M., & RASHOTTE, M. E. (1979, November). Reinforcement magnitude effects in first- and second-order autoshaping. Paper presented at the Annual Meeting of the Psychonomic Society, Phoenix, AZ.
PALYA, W. L. (1985). Sign-tracking with an interfood clock. Journal of the Experimental Analysis of Behavior, 43, 321-330.
PREMACK, D. (1965). Reinforcement theory. In D. Levine (Ed.), Nebraska Symposium on Motivation (pp. 123-180). Lincoln: University of Nebraska Press.
PREMACK, D . ( 1969, June) . Catching up with common sense or two sides of a generalization: Reinforcement and punishment. Paper presented at the Conference on the Nature of Reinforcement, Center for Research in Human Learning, University of Pittsburgh, Pittsburgh, PA.
RASHOTTE, M. E. (1981). Second-order autoshaping: Contributions to the research and theory of Pavlovian reinforcement by conditioned stimuli. In C. M. Locurto, H. S. Terrace, & J. Gibbon (Eds.), Autoshaping and conditioning theory (pp. 139-180). New York: Academic Press.
RASHOTTE, M. E., GRIFFIN, R. W., & SISK, C. L. (1977). Second-order conditioning of the pigeon's keypeck. Animal Learning & Behavior, 5, 25-38.
RESCORLA, R. A. (1979). Aspects of the reinforcer learned in second-order Pavlovian conditioning. Journal of Experimental Psychology: Animal Behavior Processes, 5, 79-95.
RESCORLA, R. A. (1980). Pavlovian second-order conditioning: Studies in associative learning. Hillsdale, NJ: Erlbaum.
RESCORLA, R. A., & WAGNER, A. R. (1972). A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In A. H. Black & W. F. Prokasy (Eds.), Classical conditioning: n Current research and theory (pp. 64-99). New York: Appleton-Century-Crofts.
Ricci, J. A. (1973). Key pecking under response-independent food presentation after long simple and compound stimuli. Journal of the Experimental Analysis of Behavior, 19, 509-516.
ROBERTS, S. (1981). Isolation of an internal clock. Journal of Experimental Psychology: Animal Behavior Processes, 7, 242-268.
SPENCE, K. W. (1956). Behavior theory and conditioning. New Haven: Yale University Press.
STADDON, J. E. R., & SIMMELHAG, V. L. (1971). The superstition experiment: A reexamination of its implication for the principles of adaptive behavior. Psychological Review, 78, 343.
TEN EYCK, R. L., JR. ( 1970). Effects of rate of reinforcement-time upon concurrent operant performance. Journal of the Experimental Analysis of Behavior, 14, 269-274.
TERRACE, H. S. (1981). Introduction: Autoshaping and two factor learning theory. In C. M. Locurto, H. S. Terrace, & J. Gibbon (Eds.), Autoshaping and conditioning theory (pp. 1-18). New York: Academic Press.
TERRACE, H. S., GIBBON, J., FARRELL, L., & BALDOCK, M. D. (1975). Temporal factors influencing the acquisition and maintenance of an autoshaped keypeck. Animal Learning & Behavior, 3, 53-62.
WALTER, D. E., & PALYA, W. L. (1984). An inexpensive experiment controller for stand-alone applications or distributed processing networks. Behavior Research Methods, Instruments, & Computers, 16, 125-134.
WICKENS, D. D. (1965). Compound conditioning in humans and cats. In W. F. Prokasy (Ed.), Classical conditioning. New York: Appleton-Century-Crofts.
ZEILER, M. D. (1977). Schedules of reinforcement: The controlling variables. In W. K. Honig & J. E. R. Staddon (Eds.), Handbook of operant behavior (pp. 201-232). Englewood Cliffs, NJ: Prentice-Hall.
(Manuscript received May 21, 1986; revision accepted for publication January 6, 1987.)
The authors gratefully acknowledge the contributions of Elizabeth Palya in all phases of this research. The paper benefited greatly from the critical reading and comments of M. D. Zeiler and M. J. Marr. Requests for reprints should be sent to William L. Palya, Department of Psychology, Jacksonville State University, Jacksonville, AL 36265.
