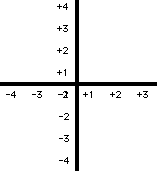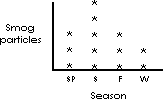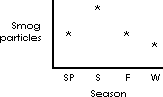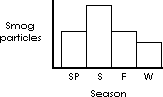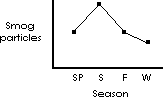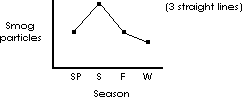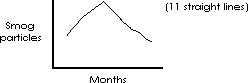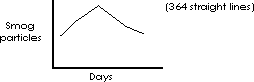CHAPTER 5
OPTIMIZATION OF RESEARCH
It is appropriate to optimize your research before assessing its adequacy. Statistics such as a “t test” or “ANOVA” provide a way to characterize or assess the reliability of research. Before assessing the reliability of your research however, it only makes sense to first take steps to maximize its reliability. Additionally, you should maximize the generality, detectability, and meaningfulness of the research
I. Reliability Maximization
Before a functional relationship or an event can be considered a fact or true it must be possible for each person to verify its existence for themselves. When you can add up a column of numbers several times and always get the same answer then in all likelihood you have added the numbers correctly. When someone else “checks” your addition and also gets the same answer then your confidence is even greater that you have the “true” answer. This is because more than one person will be able to repeat or replicate a true event. A repeatable finding is one whose controlling factors have been correctly identified. If you completely understand something you can do what it takes to make it happen or to make it stop. If you do not really understand a phenomenon you will not be able to control it reliably because it will come and go according to its true determinants and not necessarily occur in conjunction with your manipulations. If you are a creative cook you want to be able to specify a recipe so that other people can obtain the same results. Likewise, if you are a consumer of recipes then you want to be assured that if you follow the instructions you will get something good to eat. An unreliable cook is one whose meals sometimes come out right and sometimes come out no so good. If you took a person to ten psychologists and asked for a diagnosis, how much agreement would you expect? What would that amount of agreement mean? What amount of agreement do patients have a right to expect?
Several specific ways have evolved which enormously facilitate your ability to maximize reliability and thereby separate fact from fiction or to tell the truth rather than to give yourself and others. They assure that you are connected to reality by maintaining your focus on the necessity that others be able to repeat your findings. If you wish you can view this chapter allegorically. This chapter presents the rules by which you can chain a “demon.” It’s as if the variables which make things happen are invisible ghosts because they are not always immediately apparent or clearly understood. If you understand them and control for them (know their name), you can make things happen the way you want. The more ghosts you have no control over the more often your wishes will not come true. If you follow the rules in this chapter then you will be more likely to obtain productive work without the risk of being tricked by an illusion.
The use of more explicit and clearer definitions increase the reliability of a functional relationship or an event. We must clearly include the elements which are part of the meaning and exclude the elements which are not a part of the meaning. We must have explicit and precise boundaries on our definitions. See diagram on meaning (Chapter 1 section 2. c. 4.). If the set containing the elements to be measured changes, then any measure of the “set” is also likely to vary. If reliability is “getting the same answer when adding up a column of numbers multiple times,” then there must be some clear way to distinguish which “numbers” are to be added up and which are not, otherwise the answer will change. Operational/functional definitions accomplish this end. For example, often there is substantial disagreement over whether or not “punishment” works. The disagreement is empty. If we were to operationalize the definitions which the disagreeing parties were using we might hear “I showed my anger by no longer helping the person develop into a better fully functioning person. I stopped criticizing everything they did” or “20 micro volts of electricity delivered to the floor” (subject wore shoes). An example alternative to these useless definitions is “the consequence necessary to reduce the rate of the behavior by one half.” Communication must ultimately be based on operational/functional definitions.
The value of explicit definitions are apparent in other situations such as dealing with a “Philadelphia” lawyer or the “devil.” For example: You want to live forever? No problem you will live forever. What? You did not want to age? Sorry, you didn't ask for that. You must specify exactly what you mean. Imagine being in a psychiatric institution trying to get out. What would you have to do to demonstrate that you are “sane”? What if your mother were the ward supervisor? On the other hand, what if that person that you can never get along with was your ward supervisor? What if they thought it was an act? How would you get out? What would you have to do to show yourself sane? What if you found out that your roommate just got out of a psychiatric hospital after killing twelve people? What could your roommate do to demonstrate recovery? What if it were you who had just been released?
The next time you have a disagreement with someone, try defining the words at the focus of the disagreement. The disagreement will probably disappear.
Accurately and precisely describing and quantifying what is observed makes it more likely that all observers will agree on exactly what did in fact happen (i.e., that you will arrive at the truth). Quantification is the mapping of the magnitude of a thing into the vicarious system, and could be seen as modifiers for nouns such as “140 meters” or “large car” and relationships such as “2.6 times” and “bigger.” Our term must be unambiguous. Consider trying to study optical illusions with no quantification of measurement. The laws of physics would change with each new background, two things equal to a third would not necessarily be equal to each other. Large and small as modifiers could take on meaning to suit the user in their reality, imagine for example, loaning people money without quantified descriptions of the amount. Imagine a football game without a chain and the referee could just say “well it seems like a first down to me.” Recipes come out the same over and over again if the ingredients are quantified. Alchemy changed to chemistry when quantification began to be used.
Quantification or “measurement” can be seen as the conversion of some property of an event in nature into some elements in a vicarious system such as language or mathematics. The amount of information or accuracy can vary. The issue is how perfectly and completely is the listener expected to know what the speaker saw?
Quantitative relationships apparent in nature may not be available in the converted information. Information can be lost or error can be added.
Clearly the conversion to the vicarious system must index the events in some repeatable way.
The conversion must also generate information which reflects the actual attributes in nature which are of interest.
See section I E of this chapter.
Systematic errors change a measure by a constant amount in a constant direction, such as a broken ruler. Each measure will be one inch more than it should be if a one inch piece had been broken off. These errors change the mean but can be removed if they are constant and known by simply adding one inch (in this example) to the obtained measurement.
Unsystematic errors change a measure in random directions, sometimes adding, sometimes subtracting. These errors do not change the mean if they are truly random. If not random or if not specifiable, then no correction is possible.
c. Type of Measurement Operation
i. Objective Quantification
In this type of measurement, there is a mapping of events or relationships in the natural world into the vicarious system. There is great emphasis on reliability and validity across individuals. Counting objects is one example: "one chicken, two chickens, three chickens, ...... etc."
A variety of operations are available to attach a number to a comparison which occurred in nature. The evaluation of things is an example: "For me, this movie is the best and this second best."
This type of conversion places each individual in the set to be evaluated in an ordered list such as first place, second place, third place.
This type of conversion produces a value on some scale such as on a scale of 1 to 10 (e.g., rate this movie).
This conversion attaches a numerical value to each item to be scaled.
This simply identifies the item that is most xxx of the two being compared.
d. Amount of Information Retained in the Vicarious System
Groups are homogeneous only in the dimension used to define the group. In other dimensions a group can show much diversity. Even though we have separated wheat from chaff, within our bag of wheat the kernel sizes, colors, weights, or protein may vary. A pile of bricks is not the same as a pack of dogs but both the individual bricks and individual dogs differ from one another. The bricks can vary in weight and color and so can the dogs.
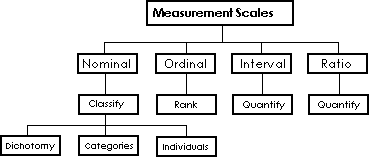
Elements of a group are frequently differentiated by assigning different elements different numerals. Assigning a “numeral” to an instance or an occurrence of something does not always mean the same thing. “Seven” is not the same as “seven” and both are completely different than “seven” and “seven” is wholly different than the previous three. There are four different things which could be meant by the numerals assigned to the elements of a group. They are essentially homonyms - same word: “seven” or “number,” but each with a different meaning. As a more familiar example imagine that someone bets you $20. that you could not use the word “lead” in a sentence correctly. The same word can mean different things depending on what was intended when the person wrote it down. The following four types of numbering systems differentiate elements of a group. Each category implies successively more about the quality or quantity of that difference. You must remember that some forms of differentiation say more about the nature of those differences than others.
If we see three people we can say they are class majestic, regal, and imperial or heavy, heavier, and heaviest , or size 30, 40, 50, or 150 pounds, 200 pounds and 250 pounds. In fact they weigh 150, 200, or 250 pounds they are, in fact, ordered in what is called a ratio scale. However we may not always have or even want every aspect of information available in nature. In our technical terminology, their ordering could be nominal, ordinal, interval or ratio depending on how much information we want to communicate. Similarly for personality except that the relationship in nature is less well known or understood. In essence then we are talking about how much information is retained in the vicarious system with respect to the variables of interest.
This is like assigning different football players different numbers. The only thing that is implied by a nominal number is that it is different from any other nominal number. You have used numbers in the same way you would use colors or shapes: the yellow glass or the red glass; the round candy or the square candy. You are using the number as a name or label. You are classifying the item. You may not put something labeled with the number 23 into the category reserved for items labeled 14 but the numbers tell you nothing other than the categories are different. You may not add, subtract, multiply, or divide the numbers meaningfully because they have no specified relationship to each other. Removing a receiver (Player #83) from one football team is not equivalent to removing the entire backfield; quarterback, halfbacks, and fullback (players numbered 12, 20, 21, 30) from the other. Any change is a difference in kind not a difference in amount. You could not find two “lucky” numbers on a roulette wheel, play their mean and be twice as lucky. The different numbers in this class could be thought of as representing a qualitative change. There are three subclasses of nominal numbers: 1) identification - each individual has a different number, e.g., ID numbers; 2) categorization, e.g., blue = 1, green = 2 and red = 3; and 3) dichotomization - all events are dichotomized into two groups, e.g., male = 1 and female = 0. The numerals can not be used in a variety of ways because they are nothing more than names and have no prespecified relationship to each other.
This system of numbers includes all the characteristics of nominal numbers. It also implies that larger numbers represent quantities that are larger than the smaller numbers. However the amount of difference between numbers is not necessarily the same. An example of this type of difference is the finish order in a race. The difference between the first and second runner may not be the same as the difference between the second and third. It is not appropriate to say that the second (2) place runner took twice as long as the first (1) place runner, and that the third (3) place runner took three times as long as the first (1) place runner.
The above figure spatially represents that the interval between the numbers in an ordinal scale may not be the same.
In this system all the properties of nominal and ordinal numbers are included. In addition, the intervals between numbers are also equal. The difference between numbers is therefore the same, for example, 36 degrees Celsius is the same amount above 35 degrees as 200 degrees is above 199 degrees. One degree is equal to one degree. However, interval numbers lack a true zero. 100 degrees is not twice as hot as 50 degrees. Using a more obvious representation (100 + x) degrees is not 2 times larger than (50 + x) degrees because the x term would also have to be considered. The figure below illustrates this effect with the arbitrary zero axis as a dotted line and the true axis as a solid line. While 4 is twice as high above the arbitrary axis as 2, it is not twice as high above the real origin. It can be seen that the true measure can be like an entire iceberg while the measure based on an arbitrary zero measure (an interval number) is like what is above the surface of the water. Twice as high above the water is not the same as twice as high altogether, if the icebergs move to fresh water their relative size above the water will change.

In this system all the above attributes of the other number systems are included. In addition, zero means the absence of the property. For example, in the Kelvin scale of temperature, 0 degrees means absolute zero, the absence of molecular motion and therefore the absence of temperature. Two degrees Kelvin is twice as hot as 1 degree Kelvin. Ratio numbers are what most people mean when they talk without qualifications about numbers.
The following figure illustrates measurement scales.
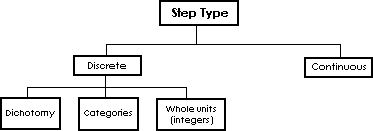
The available values which the numbers can, in principle, take; or the "step" type also varies. Some variables increase only in whole steps. They are referred to as discrete variables, e.g., family size increases only in whole steps - 1 child, 2 children, 3 children, etc. Continuous variables on the other hand can have any value in between. In actuality there are an infinite number of values between 1 and 2, e.g., weight or height can vary 100, 100.1, 100.01, 100.001, etc.
Each type of variable can therefore be categorized with: 1) type of measurement scale and, 2) type of step. For example, "discrete interval" or "continuous ratio." It would not be meaningful to use a continuous step type with a nominal or ordinal scale.
|
Continuous
|
Discrete
|
|
Ratio
|
|
|
|
Interval
|
|
|
|
Ordinal
|
not meaningful
|
|
|
Nominal
|
not meaningful
|
|
Are we directly measuring the ultimate thing of interest or are we measuring one thing and hoping that it will give us information about another?
In this case, we measure the thing directly and simply report that datum (e.g., the number of pecks in an interval.
A behavior which can be measured is used to provide information about a construct which cannot be measured directly. The rate of running is thought to tell us how much fear the person has. Fear is thought to be something "more" than simply a behavior such as running away or screaming.
iii. Behavior to Behavior Inference
In this case, one behavior is used to provide information about a second behavior. What the person says they will do is thought to tell us what they will actually do. In this case, a behavior is used to predict another explicit behavior. It could be talking about something predicting what will actually be done, or turning away predicts screaming.
Even if the “outer” boundaries of a set are precisely defined there may be variability in the elements within that set. A “group” implies necessary similarity on only one dimension. All items with the attribute are considered members of the group, those without it are excluded. When forming a group based on gender one ignores eye color. It can be seen that the rules which are used to define the group can be shifted such to include more or less variety. A group could be formed of blue-eyed males, or males between 18 and 20 with 3 years of college, or live organisms etc.
When you obtain one score from some set, you have a datum which is easy to deal with, you just write it down. When you obtain a second measure of the same attribute from that same set the situation can change, the measurement may be the same or it may differ. To use a specific example, suppose you gave an IQ test (the measure) three times to a person (the set). If they got the same score all three times then you know their IQ, the characterization of the set was easy; however, if they got three different scores then the situation is much more complicated. Do you use only the first score, only the last, or do you take the mean? What you do depends on what you believe is causing the difference. In sum, you must consider the scores as the same (one set) or different (three sets) before deciding on the value of the IQ, or in order to decide which measures apply to the person and which do not.
The first point of view is that the IQ or whatever was being measured actually remained constant and that the variation was caused by random measurement errors. In this case the average of all the measurements would be the true measurement because the measurement errors are random (sometimes above, sometimes below), and will, therefore cancel out. A random error cancels out because it varies above and below the true value equally. (A subsequent section demonstrates that the mean of a random error is equal to zero.) This is saying that each measurement is made up of the true measurement and some random error, and that the variation in the measure is caused by the error of measurement, not changes in the thing being measured.
The alternative point of view to deal with differences in measurement is to assume that the difference may be the result of an important systematic independent variable in which you should be specifically interested. For example, if you gave the tests consecutively, without any interruption, it may very well be that the person was getting tired and that the steady downward trend of the scores represented an important effect and not simply error of measurement. In this case it would not be appropriate to average the individual test scores to determine the “true” measurement.
In the behavioral sciences, if you average across groups of individuals you are, in effect, saying that any differences between those groups of individuals are only errors of measurement and that all the groups are actually the same. If you average across individuals you are assuming that individual differences are only errors of measurement and that all the individuals are actually identical. If you average across days you assume that daily variations are only error. If you average across a session you assume that no meaningful systematic effect is occurring within a session. It is very important to realize that any systematic effect which occurs across the dimension across which you are averaging becomes a confound. At best you will be ignoring a source of variance at worst your interpretation of the data will be wrong.
Obviously a decision as to what is going to be considered error or “noise” and what is to be considered a potentially important variable must be made before any averaging or grouping is done. This issue is explicitly addressed in the difference between an ideographic technique (a single subject under a wide variety of circumstances, e.g., Skinnerian research) and a nomothetic technique (comparison of the averages of the performance of groups of subjects (e.g., an approach typified by classical Hullian research). Sometimes it is argued that psychology is the study of the differences between individuals, whereas Sociology is the study of the differences between groups with the differences between individuals considered as error of measurement.
Once the determination of the appropriate level of grouping has been achieved various methods of graphic illustrations and quantitative measures for that group are then available. However, it should always be kept in mind that a choice of a unit of measure is a deliberate choice of what is to be considered irrelevant noise and what is to be considered the important subject matter of the discipline.
a. Distance as Representing Quantity
Numbers can be represented by distance from an origin along an axis. As will be seen, this simple convention (analytical geometry) has had a very large impact on our representing the world symbolically. Distance from the origin to the right or upward is considered positive while distance to the left or down is considered negative. Greater distance indicates greater quantities.
b. Space as Characterizing Group Data
Groups contain more than a single instance and therefore can be quite difficult to describe. Several ways have evolved of comprehending and depicting the information in a group of measures.
A tally graph indicates the number of occurrences or the frequency of each value by the number of marks above that value on the abscissa. The height of the stack of marks for that variable therefore also indirectly indicates the frequency of that variable. The total number of marks or asterisks, for example, in all columns then indicates the total number of occurrences. The ratio of the number of asterisks in any one column to the total number of asterisks in all columns indicates the relative frequency of that kind of asterisk occurring. For example, if there were a total of 100 occurrences, and 11 were of the specified type then 11% would then be of that type. Continuing this line of reasoning it can be seen that if things continue going like they have been you can predict that 11% of the future occurrences will also be of that type. A tally distribution therefore depicts, that of the total number of occurrences, how many were of a particular type, what proportion were that type, and if things continue as they have been, what proportion will be of that type in the future (i.e., the probability of that type occurring).
The same reasoning applies to other ways of depicting grouped data such as bar graphs, histograms, polygons, and frequency distributions. Space is used to represent important attributes. A common convention is to use height or the ordinate to indicate frequency, and the distance to the right or left of the abscissa to indicate some other dimension. In the behavioral sciences the ordinate (y) is used to represent the dependent variable while the abscissa (x) represents the independent variable. (The word "acrossissa" can be used as a memory aid. It is almost the same as abscissa and across means back and forth and contains the word cross or x.) In these cases, the height or the ordinate indicates the frequency of that variable. The total area represents the total number of occurrences. The relative area of one part of the histogram or polygon to the area of the whole histogram or polygon represents the relative frequency of an occurrence of that particular event. This ratio also represents the probability of that particular event occurring in the future if things continue as they have.
Instances can be tallied and then depicted in a figure as:
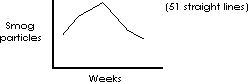
In the figure above the values for each season are indicated by the number of asterisks; any mark would serve equally well. The values are also indirectly indicated by the height of the columns.
Numerical data can be represented more abstractly, i.e., the ordinate or distance up the y axis can represent an arithmetic value. For example, the smog count for each season can be represented by the vertical positioning of a single “*” in a figure.
The figure above depicts the number of smog particles for each season in one year with only the height of the asterisk indicating the number of particles for that season.
There are two classes of figures which use this columnar form of representation. They are differentiated in terms of what the abscissa represents.
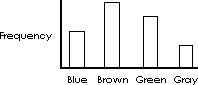
A nominal, discrete or discontinuous variable such as eye color or family size could be represented across the “x” axis. A bar graph does not imply intermediate values. There are no families with 2.5 children. There are no football players with number 66.5. The height of the bar represents the quantity of the variable represented up the “y” axis (figure below).
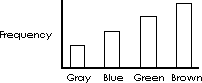
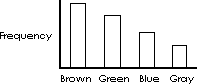
If the axis is nominal the categories along the abscissa x axis can appear in any order. Therefore no statements concerning “trends” can be made. Trends require ordinal, interval, or a ratio scale across the x axis. The axis could be rearranged to prove any trend an unscrupulous person wanted as illustrated below.
The histogram is used to depict continuous numbers such as height and weight and implies values between the categories listed along the x axis (while the bar graph does not). The bars in a histogram are continuous or are drawn together centered over their x axis value (figure below), whereas those in a bar graph are separated. Values are available between summer and winter. Because order is fixed, it is meaningful to talk about trends in a histogram.
A point may be placed above each category along the x axis at the height of the bar for that category. Clearly the points would represent the same information as the bars. If the points are in the center of each category a line can be drawn to connect them. The line then defines a frequency polygon. The frequency polygon implies quantities which would be appropriate for intermediate categories along the x axis. Therefore you may construct a frequency polygon from a histogram but may not construct one from a bar graph.
As a further example of the histogram, the smog count can be measured in finer and finer categories with each category being directly continuous with the next until a continuous curve or frequency distribution results (figures below). Note that less and less interpolation is necessary to determine a y value for an intermediate x axis value.
As can be seen in the figures, it is clear that continuing to make measurements over smaller and smaller intervals would result in an infinitely fine histogram or a continuous curve representing the frequency of occurrence (figure below).
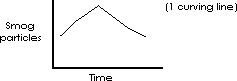

The height of the curve above any point on the abscissa represents the frequency of that particular event, just as the height of the column had represented the frequency of the event in the bar graph and histogram, and just as the number of asterisks had represented frequency in the tally record. The other relationships hold as well, in the case of the frequency distribution however you cannot meaningfully talk about the probability of an event represented by a single bar because the individual bars are infinitely small. Where a histogram allowed you to choose all the data for April by selecting a single bar a frequency distribution requires that you specify all the data from one second after midnight on March 31 to midnight April 30, i.e., specify the limits of the “bar” you want. One speaks of the frequency of all events contained between point A and Point B on the x axis, where A and B can be any position along that axis. A histogram has preselected points A and B.
Measures of central tendency specify a value which can be taken as the x value which is representative of all values in the distribution. The difference between various measures of central tendency result from the difficulty of a single formula providing a meaningful single summary value for all possible distributions.
These are measures which indicate how the values within the distribution differ from one another. Distributions which differ with respect to their dispersion are spread out or are bunched together more.
Distributions are not always uniformly symmetrical and gaussian. Distributions can be sloped to one side to a greater or lesser extent, or can be sharply peaked or flat.
d. Relationship Between Subgroups
There may also be specific relationships between the elements in the subgroups making up the set. For example, in the set "people," height and weight are related, whereas IQ and shoe size are not related.
e. Other Methods of Quantifying Group Data
i. "Statistics" as Representing Groups
If you look at the difference between means of random groups divided by the average of their variances you get t, etc.
x
x
A measure determined by several different independent methods based on different assumptions is much more likely to be reliable than a measure determined by only one method. If you have an inferred measure like response strength and it is equally well measured by latency, rate, errors, force of pull, and duration, then it is more likely to be reliable than if it were measured only in one way.
If you make a statement of a functional relationship based on only an extremely narrow specific group of subjects, kind of apparatus, or procedure it is possible for it to be altered by even a small change in any number of variables. Statements of wide generality which fit many situations are less likely to be disrupted by unforeseen events. More broadly based statements are more reliable. Somewhat like Weber's fraction: the larger the base the larger a difference must be to cause a change. An anomalous change in the illumination at noon doesn't change the exposure required for a picture by very much.
Unfortunately, all possible variables are not reported in every research paper. Some variables are not made explicit because they are thought to be obvious and well known, or are common to normally accepted research practice, or to everyone's research style. People familiar with a particular area are likely to know through experience what to control as a matter of professional research practice even though every detail does not appear in print due to publication costs. This absence is not because of carelessness or ignorance but rather the recondite nature of professional research. Reliability can be increased by being aware of the important variables in a situation which are not explicitly pointed out. Apprenticeships or practicums are extremely important for this reason.
For a measure to be reliable, you must measure what you think you are measuring. You must be correctly connected to reality.
For example, if you read a humidity gauge and believe you are reading a temperature gauge it is extremely unlikely that people will be able to replicate your effect when they follow your instructions to read a temperature gauge. If you view a thermometer from an extreme angle and get a parallax error in your measure, then your measure will not be replicable by either people who measure the temperature correctly or who measure it with their own inaccuracy. You must be correctly connected to reality.
If you measure something indirectly you must assure yourself that you have measured what you thought you measured. Indirect measures are prone to error, invalidity, and unreliability. Use direct measures whenever possible. If you ask people what they will do in a crisis, you cannot automatically infer that they will do exactly that. In actuality what they do is an entirely open question. If you claim you are terrifying people by saying 'boo' or if you claim you are measuring fear by measuring withdrawal, you must verify that your construct is in fact the thing being measured. Researchers have put pigeons on a schedule where a key peck could avoid shock. They found that pigeons would not peck to avoid shock. They did not find that pigeons won't avoid shock. They will fly away to avoid shock, as anyone who had chased pigeons in the park will attest to.
If you document what you do carefully and follow the procedure explicitly then it is likely that someone else following the same directions will obtain the same results. If you do not document what you did correctly it is unlikely that their cake will turn out, when they use your recipe. It’s also obvious that any statistical tests of reliability must be calculated correctly.
The experimental design must allow you to “subtract out” or “cancel” all potential alternate explanations for the effect. You must have what has come to be called internal validity (see research design section in Chapter 4 IV. B.).
The statistical treatments which are applied to the data generated by research require that certain assumptions be met. For that reason research which will be analyzed by statistics must be designed with its subsequent statistical analysis in mind. A particularly troublesome problem is the use of the statistic appropriate for the type of variables in the research. See The Conceptual Precursor on the Classification of Variables section (Chapter 5 B. 1. d.). The level of reliability specified by a statistical test is meaningless if done on data which violates the assumptions of that statistic. A sporting record is meaningless if it were obtained in a situation which violates the assumption of the sport. A quarterback who gains 700 yards in a single game by driving to the end zone in a golf cart has set no record. A "no hitter" is no record if a greased ball was used.
A technologically sophisticated experiment exerts as much control over confounding variables as possible to minimize their impact. It also measures variables in the most sophisticated way possible to maximize the accuracy and precision of the obtained measures. Higher technology provides better tools to enable correct assessment of the actual controlling variable and provides the power to reproduce the effect by accurately creating or recreating the controlling conditions. Using a scale to measure weight is more reliable than a subjective estimation. Data complete computerized or "untouched by human hands" is be less likely to contain errors.
An extremely strong effect is likely to recur, whereas a very small effect is more likely to be overshadowed by noise, or to have arisen by chance in the first place. You can obtain large signal to noise ratios by choosing to study strong effects, by using strong treatments, or by reducing the noise in the experiment.
You do an experiment in order to find out more about the variable than you knew before. You do an experiment by manipulating the independent variable to assess its effect on the dependent variable. This seems very simple. Unfortunately many things can confound the interpretation of the results.
In any experiment, many possible confounding influences may exist. If you do not control them, some alternative explanations are possible for your results. If this is the case, your experiment is of little value because you cannot be sure why things happened the way they did. It is crucial to understand that if an alternative explanation for the results is available, what you have is a "likely story" and that is all. To put the shoe on the other foot, imagine being innocent but being on trial for your life. The prosecutor has put together a plausible scenario with you as a murderer. You would, of course, want to point out the equally plausible scenario in which you are innocent. We have all seen at least one movie with basically this very plot. The American constitution demands "beyond a shadow of a doubt" for that very reason. The innocent are protected from prosecutors that ignore alternative scenarios, and from hyped-up lynch mobs. For that same reason, the community should be protected from sloppy therapists or experimenters that ignore alternative explanations and get away from the facts. When you are interested in truth you must make sure that alternative explanations are not possible. Otherwise, there is a reasonable doubt and, you have not proven a thing. You should be no more willing to bet someone else's life on a likely story than you would risk your own.
By deliberately manipulating the occurrence of its precursors the true cause of an event can be easily established. If all events except the “cause” are allowed to occur and the “result” does not occur, and if only the cause is added and the “result” then occurs; and if the removal of the cause again terminates the result then a cause-effect relationship has been established. If you were trying to discover to what you were allergic, you would do similar research, adding and subtracting items from your environment until you found what was causing the problem. Obviously, it is very important to assure yourself that you have not confounded your experiment in some way by adding or subtracting more than one thing at a time. You may wonder why you would want to bring your allergic reaction back. But, only by doing that will you be sure of its cause and only then will you be relatively sure you are not avoiding some object inappropriately. What if you had a cold rather than an allergy and you got better right after you spent all your money? For the rest of your life you would think you were allergic to money.
Obviously, the best method of dealing with confounding variables is to remove or eliminate them altogether. If you were measuring IQ, and found that some people were taking the test while drinking coffee you could methodologically eliminate the confounding variable by not allowing anyone to drink coffee during the test. In the pan balance example, “A” would be taken from each side.
Or, you could methodologically eliminate the difference caused by the coffee by having everyone drink coffee (putting an ”A” on both sides of the pan balance) or by considering the coffee drinkers separately from the nondrinkers in your analysis of the results. Alternatively, you could eliminate the effect statistically by subtracting the effect that the coffee had on the test from scores of those who did drink it. This correction requires of course that the addition to each score be known, and that it be the same for each individual.
b. Equalization or Matching
A different method is to equalize the effect of the confounding or extraneous variable. You could ensure that each group consumed the same amount of coffee as a group or that for each person in the experimental group that drank one cup of coffee there was a person in the control group that also drank one cup of coffee. For each person that drank two cups of coffee in the experimental group there was a person that drank two cups in the control group, and so on. In the pan balance example that would be to assure that for each “A” on one side; there was an “A” on the other side.
You could also explicitly balance the two groups. For example, you could have two basketball teams play several games switching players after each game until they ended each game in a tie. This procedure would explicitly balance the groups with respect to basketball playing ability. You could then give the treatment to one team to assess its effects on basketball playing. For the IQ testing example the coffee confound could be explicitly balanced by moving the coffee drinkers around until both groups had the same mean IQ. Then you could administer the treatment of interest to one group, with the assurance that the two groups were equal with respect to the effects of coffee on IQ. With balancing there may not be any equivalent individuals in the two groups, e.g., Group 1 has IQ 200 and 100 while Group 2 has IQ 150 and 150. In the pan balance example this would be moving things back and forth between the pans until they were the same regardless of what and how many things were on each side. You would then add the unknown that you wanted to weigh to one side.
d. Balancing by Theoretical Notions
There are occasions when equalization or explicit balancing is not applicable or possible. In that case you can still try to balance the two groups based on what you think should be equal. For example, you could counterbalance the groups by assigning the best and worst individual to one group and the two middle individuals to the other group.
The problem with balancing in this way is that a “linear” effect of the variable is usually assumed, i.e., it is generally assumed that the average of the middle two intensities of each variable is equal to the average of the outer two, e.g., in a series of 1,2,3,4, it is assumed that 1 + 4 over 2 is equal to 2 + 3 over 2, (as it does in this example which was chosen to work out). In the explicit balancing example, the distribution of IQs is the result of the empirical process of balancing whereas with balancing based on theoretical notions, we sort subjects into groups that we have some reason to believe are equal, but for which we have no proof. We have no evidence that the average of one and four cups of coffee is the same as the average impact of 2 and 3 cups of coffee or that a team which contains a person with an IQ of 200 and one with an IQ of 0 is the same as a team with two people with an IQ of 100. In the pan balance example, this would be “believing” that the things in one pan weighed the same as the different things in the other pan because they should be equal.
Members of each group can be selected at random. In this way the groups will tend to be equalized by the action of chance. In the pan balance example, this would be placing 60 handfuls of randomly selected stuff from a barrel on one side and 60 handfuls of randomly selected stuff from the same barrel on the other because the random variations in the items on each side should cancel out. Amazingly enough (given about 30 or more elements), random assignment will tend to equate any number of variables simultaneously. In fact it will equate variables which you are not even aware of. Any other method requires perfect knowledge of potentially confounding factors and a very extensive task of determining how to assign elements such that the overall groups are equated. Additionally, most statistics are designed to assess the likelihood of two groups selected at random differing by the obtained amount. For that reason alone it is advisable to select groups by random assignment if subsequent statistical treatment assumes it.
The chosen dependent variables should be viewed in terms of dimensions which are actually controlling those changes. This is an important element in the post hoc reorganization of data discussed in Chapter 4 IV. A. 2. a. Little long term, real consistency would be obtained if a psychotherapy were evaluated in terms of the shoe size of its recipients. The apparent success of the therapy with children and its lack of success with adults would be spurious. Even though shoe size tends to increase with time and therefore correctly indexes presumed increasing psychological health in many clients, it also incorrectly indexes the health of many clients who are getting worse or showing no change. Psychotherapy should be judged in terms of some consensually validatable and relevant dependent measure such as the percentage of successful social interactions or whatever is agreed to be what psychological health means. Lack of operational/functional definitions of what health is allows ignorant and unscrupulous psychotherapists to believe, or at least claim to be effective, when they are not; because of an unclear or an erroneous dependent measure. If it is a proper measure other people will find the same thing, it will be reliable.
The independent variable must also be chosen with care. The correct or valid identification of factors which are influencing the dependent measure makes sure that relevant but unrecognized variables will not be inadvertently changed or left out during attempted replication. If the actual controlling variable was not correctly specified it may not be included in an attempt to replicate. The original finding will, as a result, be unreliable. Replication by other laboratories is essential for this reason. It assures that the relevant factors have been specified as the independent variable. It is unlikely that the two laboratories or researchers have the same “hidden” factors. They would be unable to replicate an effect if the specified independent variable were not the cause.
Frequently, there is overall consistency in data while there appears to be little local consistency, or vice versa. This is the “forest-trees” problem. A comparison of whole forests may show consistent effects, even through a comparison of each tree is confusing or vice versa. Viewing the data within a broader or narrower context may increase reliability. Additionally, rescaling the data with a transformation such as a log transformation may allow the orderly nature of the data to be more apparent.
Whether or not consecutive measures of the same thing have the same value or not is determined by the measuring instrument. An instrument which is extremely coarse will provide measures which differ very little and which are therefore extremely reliable. For example, if you measured your weight on a scale for tractor trailers you would find that you always weighed the same no matter what you ate. The instrument would provide data which was extremely reliable in that it was always the same. Unfortunately it would be of little use. At the opposite extreme, an instrument which is extremely fine will obtain data which varies widely and which are not at all reliable, and therefore do not emphasize the similarity of the events. For example if you measured your weight on an analytical balance accurate to millionths of a gram you would find that your weight varied considerably as you breathed and as the floor vibrated. A compromise must be struck between ridiculously gross measures which are very reliable yet are not useful because they do not detect meaningful differences; and ridiculously fine measures that are not useful in that they vary so widely that they mask similarity. This can be roughly illustrated with the scale on the following three figures.
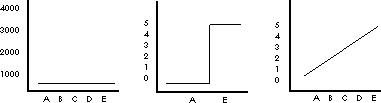
A researcher can maximize the reliability of the findings by correctly choosing questions or structuring the situation to dramatically expose the controlling variables. This is the art of good research. It is the degree to which you can identify a clear boundary condition which varies from one category to the other with a change in the independent variable. Building on the underwater steam shovel metaphor from the first chapter, this is simply your skill in finding the boundary between the boom and the mud by choosing the nature of your probe how you jab around and how well you interpret what you feel. For example when trying to guess letters in a game like "Wheel of Fortune," some letters are more likely to be right than others.
A finding which is consistent with great sections of the interlocking body of knowledge and that is not incompatible with any basic understandings is more likely to be reliable than a finding which is inconsistent with much of our acquired knowledge. A finding which is consistent with a great body of knowledge is more believable than one which is simply unlikely to occur by chance alone. Part of the task of the discussion section of a journal article is to establish continuity with the theoretical net for this very reason. Keep in mind that your task is to make sense out of the environment, not to show how you cannot make sense out of it. "Scientific glory" goes to the person who makes sense out of a finding, not to someone who throws out a fact which may be true and important or may be an error and irrelevant. Do not simply search for an anomalous finding. Rather try to advance understanding. A retardate can "not make sense" out of almost any finding.
Data are being replicated continually and used to design more complex experiments. When data can be repeated and/or used to predict new results, its reliability is substantiated by definition. This is especially true when investigators with opposing theoretical views replicate the finding.



Date Last Reviewed: November 17, 2002